Razón geométrica

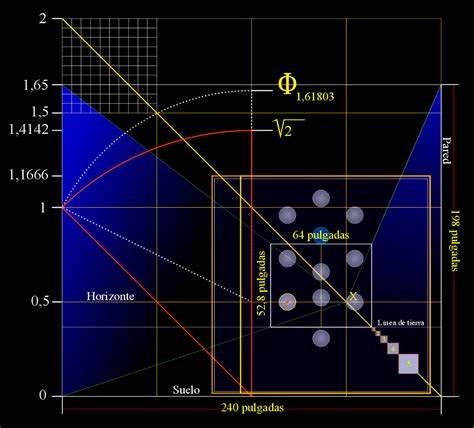
En las matemáticas, la razón es una relación binaria entre magnitudes (es decir, objetos, personas, estudiantes, unidades del SI, etc.), generalmente se expresa como "a es a b" o a:b. En el caso de números toda razón se puede expresar como una fracción y eventualmente como un decimal.[cita requerida]
En ocasiones se habla de razón aritmética y razón geométrica en el contexto de las progresiones aritméticas y progresiones geométricas, respectivamente. En los dos casos, la razón se entiende como la relación entre dos términos consecutivos de la sucesión, denominados antecedente y consecuente, siendo esta relación la diferencia en el caso de las progresiones aritméticas y el cociente en el caso de las progresiones geométricas. Tradicionalmente se ha denominado exponente o exponente de la razón al número resultado de esta diferencia o cociente. En general, se entiende por razón el cociente adimensional entre dos números, y es en este sentido que se habla de razón de aspecto en una imagen o de la razón profesor-alumnos en un centro educativo.
La razón geométrica es la comparación de dos cantidades por su cociente, donde se ve cuántas veces contiene una a la otra. Solo si las magnitudes a comparar tienen la misma unidad de medida la razón es adimensional.
Una razón «X:Y» se puede leer como «X sobre Y», o bien «X es a Y».
El numerador de la razón (es decir, el X) se llama antecedente y al denominador (el Y) se le conoce como consecuente.

18/6 representa la razón de 18 entre 6, que es igual a 3 (18 tiene tres veces 6). Su razón geométrica es 3, su antecedente 18, y su consecuente 6. 20/2 representa la razón de 20 entre 2, que es igual a 10 (20 tiene diez veces 2). Su razón geométrica es 10, su antecedente 20, y su consecuente 2.
La razón aritmética[cita requerida] de dos cantidades es la diferencia (o resta) de dichas cantidades. La razón aritmética se puede escribir colocando entre las dos cantidades el signo . o bien con el signo -. Así, la razón aritmética de 6 a 4 se escribe: 6.4 o 6-4.
El primer término de una razón aritmética recibe el nombre de antecedente y el segundo el de consecuente. Así en la razón 6-4, el antecedente es 6 y el consecuente 4.
Como la razón aritmética de dos cantidades no es más que la resta indicada de dichas cantidades, las propiedades de las razones aritméticas serán las propiedades de toda suma o resta.
Si al antecedente se le suma o resta una cantidad la razón aritmética queda aumentada o disminuida dicha cantidad.
Si al consecuente de una razón aritmética se suma o se resta una cantidad cualquiera, la razón queda disminuida en el primer caso y aumentada en el segundo en la cantidad de veces que indica dicho número.
Una "proporción aritmética" es una expresión de la relación de igualdad entre 2 razones. Las proporciones aritméticas se pueden representar de dos maneras distintas:
y se lee "a es a b como c es a d".
Los términos primero y cuarto de una proporción aritmética reciben el nombre de extremos, mientras que los términos segundo y tercero se denominan medios. Así sea la proporción aritmética 10:5 = 8:4. Los términos 10 y 4 (son extremos) y, 5 y 8 (son medios).

Las proporciones aritméticas cuyos medios no son iguales reciben el nombre de proporciones aritméticas discretas.
La razón simple de tres números a, b y c, expresada (abc), se define como el cociente de las diferencias entre el primero y cada uno de los otros dos.
La razón doble de cuatro números a, b, c y d, expresada (abcd), se define como el cociente entre la razón simple de a, c y d y la razón simple de b, c y d.
Escribe un comentario o lo que quieras sobre Razón geométrica (directo, no tienes que registrarte)
Comentarios
(de más nuevos a más antiguos)
Aún no hay comentarios, ¡deja el primero!


