Quicksort

El ordenamiento rápido (quicksort en inglés) es un algoritmo de ordenacion creado por el científico británico en computación C. A. R. Hoare.

El algoritmo trabaja de la siguiente forma:

Como se puede suponer, la eficiencia del algoritmo depende de la posición en la que termine el pivote elegido.

No es extraño, pues, que la mayoría de optimizaciones que se aplican al algoritmo se centren en la elección del pivote.

Supongamos que el número de elementos a ordenar es una potencia de dos, es decir, ${displaystyle n=2^{k}}$ para algún natural ${displaystyle k}$. Inmediatamente ${displaystyle k=log_{2}(n)}$, donde k es el número de divisiones que realizará el algoritmo.

En la primera fase del algoritmo habrá n comparaciones. En la segunda fase el algoritmo instanciará dos sublistas de tamaño aproximadamente n/2. El número total de comparaciones de estas dos sublistas es: 2(n/2) = n. En la tercera fase el algoritmo procesará 4 sublistas más, por tanto el número total de comparaciones en esta fase es 4(n/4) = n.

En conclusión, el número total de comparaciones que hace el algoritmo es:

${displaystyle n+n+n+.....+n=kn}$, donde ${displaystyle k=log_{2}(n)}$, por tanto el Orden de Complejidad del algoritmo en el mejor de los casos es ${displaystyle O(n.log_{2}n)}$.

El algoritmo básico del método Quicksort consiste en tomar cualquier elemento de la lista al cual denominaremos como pivote, dependiendo de la partición en que se elija, el algoritmo será más o menos eficiente.

Una idea preliminar para ubicar el pivote, en su posición final sería contar la cantidad de elementos menores que él, y colocarlo un lugar más arriba, moviendo luego todos esos elementos menores que él a su izquierda, para que pueda aplicarse la recursividad.

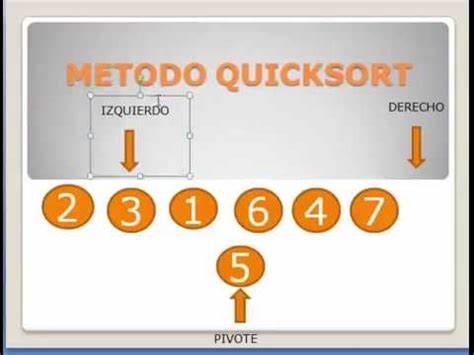
Existe, no obstante, un procedimiento mucho más efectivo. Se utilizan dos índices: i, al que llamaremos índice izquierdo, y j, al que llamaremos índice derecho. El algoritmo es el siguiente:

Como se mencionó anteriormente, el algoritmo quicksort ofrece un orden de ejecución O(n²) para ciertas permutaciones "críticas" de los elementos de la lista, que siempre surgen cuando se elige el pivote «a ciegas». La permutación concreta depende del pivote elegido, pero suele corresponder a secuencias ordenadas. Se tiene que la probabilidad de encontrarse con una de estas secuencias es inversamente proporcional a su tamaño.

Nota: Los tres parámetros de la llamada inicial a Quicksort serán array[0], 0, numero_elementos -1, es decir, si es un array de 6 elementos array, 0, 5

En el siguiente ejemplo se marcan el pivote y los índices i y j con las letras p, i y j respectivamente.

---