Números pares e impares

En matemáticas, un número par es un número entero que es divisible entre dos.^[1]​ Se trata de un número entero que se puede escribir de la forma: 2k (es decir, divisible de manera entera entre 2), donde k es un entero (los números pares son los múltiplos del número 2). Los números enteros que no son pares se llaman números impares (o números menores), y pueden escribirse como 2k+1.^[2]​

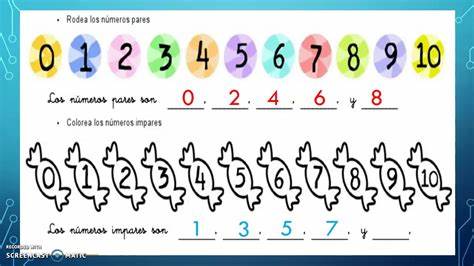
Los números pares son:

y los impares:

La paridad de un número entero se refiere a su atributo de ser par o impar.^[3]​ Comparativamente, dos números son «de la misma paridad» si al dividirlos entre 2, el resto es el mismo, por ejemplo: "2" y "4", o "3" y "7"; son «de la misma paridad». Por el contrario los números "23" y "44" son «de distinta paridad».

Esta se complementa por una fácil fórmula:

par + par = par | par + impar = impar | impar + impar = par

Si la base de numeración utilizada es un número par (por ejemplo, base 10 o base 8), un número par podrá reconocerse si su último dígito también es par. Por ejemplo, el siguiente número en base 10:

es par ya que su último dígito: 3, también es par. Lo mismo sucede con el siguiente número en base 6:

Si la base del sistema de numeración es impar (3, 5, etc), el número será par si el número de dígitos con cifra impar es par, en cualquier otro caso el número será impar. Por ejemplo, en base 3:

es impar, dado que el uno es la única cifra impar, mientras que:

Como el 3 y el 1 son impares, hay un número par de cifras impares y el número es par.

El cero es un número par, cumple con la definición así como con todas las propiedades de los números pares.

En el libro 7 de los Elementos de Euclides^[5]​ (definiciones 8 a 10), vienen definidas unas clases de números que, aunque hoy en desuso, han sido citadas de forma recurrente en libros históricos de matemáticas.

Observaciones:

Algunas fuentes, tales como Dorado contador. Aritmética especulativa y práctica (1794)^[8]​ y el más reciente, Enjambre matemático,^[9]​ utilizan otra definición para los números parmente pares: no se trata de los que son productos de dos pares, sino de los que sólo se pueden expresar como producto de dos pares (exceptuando, por supuesto, el producto de sí mismos por uno). Según esta definición, los números parmente pares son exactamente las potencias de 2. Asimismo, definen el número parmente impar como el múltiplo de una potencia de 2 por un número impar e introducen el concepto, ausente en la obra de Euclides,^[9]​ de número imparmente par como un número que es doble de un número impar. La definición del número imparmente impar no sufre variación.

El libro Llave aritmética y algebrayca^[10]​ utiliza las primeras definiciones y explica el caso de que haya números que son simultáneamente parmente pares y parmente impares. Esta definición, además, queda reforzada en la proposición 32 del libro 9 de los Elementos,^[5]​ que explica así: «Cada uno de los números (que es continuamente) duplicado a partir de una díada es solamente un (número) parmente par.»

Sea el conjunto de los pares ${displaystyle 2mathbb {Z} }$ = {0, 2, 4, 6, 8, 10,...2n..., n cualquier natural}.^[11]​

el elemento a es primo en 2Z si no existe un elemento de 2Z que lo divida.

Por ejemplo, 6, 10, pues no hay elemento de 2Z que lo dividan parmente.

Fuera de los primos en sentido par, los otros números tienen más de dos divisores

48 y 32 tienen como divisores comunes 2, 4, 8, y 16 no, porque no divide parmente a 48^[13]​

El mayor de los divisores comunes de dos elementos de ${displaystyle 2mathbb {Z} }$ se llama máximo común divisor (m.c.d.).

---