Curva de Koch

El copo de nieve de Koch, también llamado estrella de Koch o isla de Koch,^[1]​ es una curva cerrada continua pero no diferenciable en ningún punto descrita por el matemático sueco Helge von Koch en 1904 en un artículo titulado «Acerca de una curva continua que no posee tangentes y obtenida por los métodos de la geometría elemental».^[2]​ ^[3]​

En lenguaje actual, diríamos que es una curva fractal. Su construcción más simple se realiza mediante un proceso iterativo que se inicia partiendo en tres un segmento de recta e insertando dos más en el tercero medio a manera de un triángulo equilátero, el proceso se repite infinidad de veces. La curva de Koch es un caso particular de curva de De Rham.

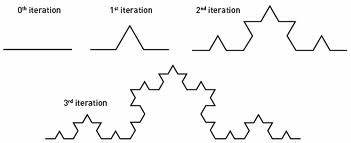
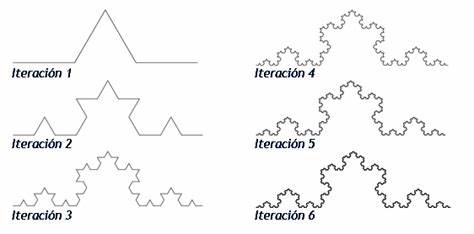
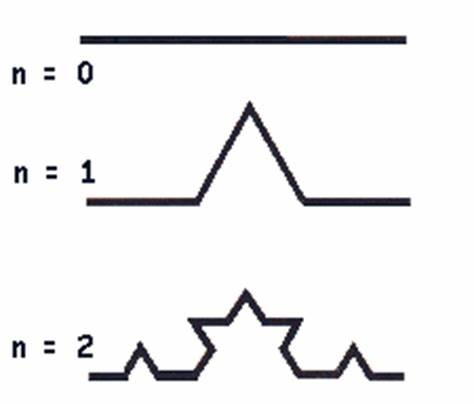
Veamos el proceso que lleva a sustituir cada lado por la llamada curva de Koch: Se toma un segmento, se lo divide en tres partes iguales, se remplaza la parte central por dos partes de igual longitud haciendo un ángulo de 60 grados. Luego, con los cuatro segmentos, se procede de la misma manera, lo que da lugar a 16 segmentos más pequeños en la segunda iteración. Y así sucesivamente. La figura representa las seis primeras etapas de la construcción. La última curva es una buena aproximación de la curva final.

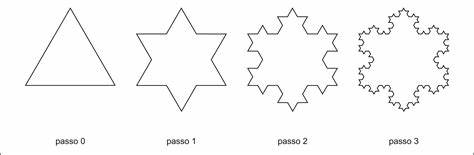
Tres de estas curvas unidas forman el copo de nieve de Koch y el anticopo de nieve de Koch:

La curva de Koch se puede expresar en el sistema Lindenmayer

Aquí, F significa «continua dibujando», + «gira 60 grados a la derecha, y - «gira 60 grados a la izquierda» (ver gráficas tortuga)

Cada iteración multiplica el número de lados en el copo de nieve de Koch por cuatro, por lo que el número de lados después de las iteraciones n viene dado por:

Si el triángulo equilátero original tiene lados de longitud s, la longitud de cada lado del copo de nieve después de las iteraciones n es:

un inverso potencia de tres múltiplo de la longitud original. El perímetro del copo de nieve después de las iteraciones n es:

La curva de Koch tiene una longitud infinita, porque la longitud total de la curva aumenta en un factor de 4/3 con cada iteración. Cada iteración crea cuatro veces más segmentos de línea que en la iteración anterior, siendo la longitud de cada uno 1/3 la longitud de los segmentos en la etapa anterior. Por lo tanto, la longitud de la curva después de n iteraciones será (4/3) ⁿ veces el perímetro del triángulo original y es ilimitado, ya que n tiende al infinito.

Como el número de iteraciones tiende al infinito, el límite del perímetro es:

donde |4/3| > 1.

Existe una medida dimensional ln 4/ln 3, pero hasta ahora no se ha calculado. Solo se han inventado los límites superior e inferior. ^[4]​

En cada iteración se agrega un nuevo triángulo a cada lado de la iteración anterior, por lo que el número de triángulos nuevos agregados en la iteración n es:

El área de cada nuevo triángulo agregado en una iteración es 1/9 del área de cada triángulo agregado en la iteración anterior, por lo que el área de cada triángulo agregado en la iteración n es:

donde a₀ es el área del triángulo original. El área nueva total agregada en la iteración n es por lo tanto:

El área total del copo de nieve después de las iteraciones n es:

Colapsando la suma geométrica da:

El límite del área es:

donde |4/9| < 1.

Por lo tanto, el área del copo de nieve de Koch es 8/ 5 del área del triángulo original. Expresado en términos de la longitud lateral s del triángulo original, esto es: ^[5]​

La característica anterior, típica de muchas curvas fractales, añadida al hecho de que la curva da la impresión de tener cierto espesor a causa de sus constantes cambios de dirección, sugiere que esta figura, en algún sentido, no es unidimensional. Para ello usaremos una generalización del concepto de dimensión: la dimensión fractal de Hausdorff.

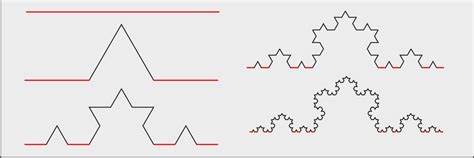
Su dimensión de Hausdorff tiene que estar entre 1, la de una recta, y 2, la del plano. Para hallarla miremos la última curva: Si agrandamos (mediante una homotecia) tres veces la sección A'B' obtenemos exactamente la sección AB. En la curva final, obtendríamos la sección A'C, es decir cuatro veces la sección inicial.

Se sabe que una homotecia de razón tres multiplica las longitudes por 3, las superficies por 3² = 9, los volúmenes por 3³ = 27, y más generalmente, el "volumen" de objeto de dimensión d por 3^d. Entonces tenemos 3^d = 4 para el copo de Koch, lo que da:

${displaystyle d={frac {ln 4}{ln 3}}approx 1,26186dots }$

La dimensión de homotecia anterior coincide en este caso con la dimensión fractal de Hausdorff. La configuración opuesta-complementaria de un copo de nieve de Koch o copo de nieve fractal suele ser denominada anticopo de nieve.

Existen múltiples variantes de la curva de Koch, cambiando el ángulo de 60°, el triángulo equilátero por otro polígono o el conjunto inicial.

Programa utilizando el módulo turtle, incluido en la biblioteca estándar de Python^[6]​

---